"Mujoco 번역"의 두 판 사이의 차이
Kim135797531 (토론 | 기여) 잔글 |
Kim135797531 (토론 | 기여) 잔글 |
||
| (같은 사용자의 중간 판 하나는 보이지 않습니다) | |||
| 2번째 줄: | 2번째 줄: | ||
DISCLAIMER: This is an unofficial translation of mujoco.org/book and may be mistranslated. Will be removed if any problem. | DISCLAIMER: This is an unofficial translation of mujoco.org/book and may be mistranslated. Will be removed if any problem. | ||
=계산 (Computation)= | = 계산 (Computation) = | ||
=모델링 (Modeling)= | |||
==Solver 파라미터 (Solver parameters)== | == 파라미터 (Parameters) == | ||
<math>\Omega</math> = 제약 집합 | |||
여기서 <math>( R, a^* )</math>가 모델 파라미터로부터 어떻게 계산되는지 설명한다. 선택된 파라미터화가 make sense하기 위하여, 우리는 먼저 이 수치들이 어떻게 다이나믹스에 영향을 미치는지 이해해야 한다. 우리는 (4)의 제약되지 않은 minimizer, <math display="block">f^+ = (A+R)^{-1} (a^* - a^0 )</math>에 대해 설명한다. 만약 <math>(f^+ \in \Omega )</math> 이라면, <math>f^+ = f</math>가 우리 모델에서 생성되는 실제 제약 힘이다. 특정 시간에 활성 상태인 <math>\Omega</math>(제약)의 부분집합의 크기는 일반적으로 작고, 또한 실제로 이 경우만이 우리가 분석할 수 있기 때문에 이 경우에 집중할 것이다. 제약 다이나믹스 (5) 안의 <math>f^+</math>를 치환하고 항들을 재배열하면 <math display="block">a^1 = A (A+R)^{-1} a^* + R (A+R)^{-1} a^0</math>가 된다. 따라서 제약된 가속도는 제약되지 않은 가속도와 참조(reference) 가속도 사이에서 보간된다. 특히, 한계 <math>R \to 0</math> 에서는 우리는 강한 제약을 갖고 <math>a^1 = a^*</math>이 되지만, <math>R \to \infty</math>에서는 우리는 무한대로 부드러운 제약 (예: 제약 없음)을 갖고 <math>a^1 = a^0</math>이다. 따라서 보간을 직접 제어하는 모델 파라미터를 도입하는 것이 자연스럽다. 우리는 이 파라미터를 ''임피던스(Impedance)''라고 부르고 <math>d</math>라고 표기한다. 이것은 <math>n_C </math>차원의 벡터이고 각 요소별로 <math>0<d<1</math>를 만족한다. 일단 이것이 지정되면, 우리는 정규화기(regularizer)의 대각 요소를 <math display="block">R_{ii} = \frac{1-d_i}{d_i} \hat{A}_{ii}</math>로 갖는다. 참고로 우리는 실제 <math>A</math> 행렬의 대각성분이 아니라 근사치를 사용하고 있다. 이것은 우리가 sparse solver나 inverse dynamics에서 A를 계산하고 싶지 않기 때문이다. 이 근사(대각 성분으로 제한된)는 모델이 초기 설정값 mjModel.qpos0일 때의 모든 "엔드 이펙터" body의 inertia, joint, tendon를 사용해서 구성된다. 이러한 수치는 컴파일러에서 계산된다. 만약 우리의 근사치가 정확하고, <math>A</math> 행렬 자체가 대각이라면, 각 스칼라 제약의 가속도는 <math display="block">a^1_i = d_i a^*_i + (1-d_i) a^0_i</math>을 만족할 것이고 우리는 원하는 보간 효과를 얻을 수 있을 것이다. 물론 이는 일반적으로 적용되는 것은 아니지만, 여기서의 목표는 제약 모델에 대한 합리적이고 직관적인 파라미터화를 구성하고 확장을 올바르게 수행하는 것이다. | |||
다음으로 참조(reference) 가속도의 계산 방법을 설명한다. 이미 언급한 바와 같이, ''damping(감쇠)'' 및 ''stiffness(강성)'' 계수에 의해 매개 변수화된 스프링 댐퍼 모델을 요소별로 사용한다:<math display="block">a^*_i = -b_i (J v)_i - k_i r_i</math>r은 위치 residual (elliptic cones의 마찰 차원과마찰 손실이 0인 경우) 이고, <math>Jv</math>는 제약에 투영된 joint 속도임을 상기하자; index 표기는 투영된 속도 벡터의 한 성분을 참조한다. | |||
요약하면, 사용자는 임피던스 계수 <math>0<d<1</math>, damping 계수 <math>b > 0</math>과 stiffness 계수 <math>k > 0</math> 들의 벡터를 지정한다. 그 뒤 위와 같이 <math>R, a^*</math>는 MuJoCo에 의해 계산되고, 선택된 최적화 알고리즘이 문제 (4)를 풀기 위해 적용된다. Modeling 챕터의 Solver parameters 섹션에서 설명하듯이, MuJoCo는 임계 damping에 도달하도록 <math>d, b, k</math> 설정을 위한 추가적인 자동화를 제공하거나, 거리에 따라 바뀌는 <math>d</math>를 통한 부드러운 contact 레이어를 제공한다. | |||
= 모델링 (Modeling) = | |||
== Solver 파라미터 (Solver parameters) == | |||
Computation 챕터의 Solver 파라미터 섹션에서 MuJoCo의 제약의 행동을 결정하는 수치 d, b, k의 수학적 알고리즘적 의미를 설명했다. 여기서 우리는 그것을 어떻게 설정하는지 설명한다. | Computation 챕터의 Solver 파라미터 섹션에서 MuJoCo의 제약의 행동을 결정하는 수치 d, b, k의 수학적 알고리즘적 의미를 설명했다. 여기서 우리는 그것을 어떻게 설정하는지 설명한다. | ||
| 17번째 줄: | 28번째 줄: | ||
Computation 챕터에서와 조금 다른 표기법을 사용하여, | Computation 챕터에서와 조금 다른 표기법을 사용하여, | ||
* a1을 가속도, | * a1을 가속도, | ||
* v를 속도, | * v를 속도, | ||
| 25번째 줄: | 37번째 줄: | ||
앞서 분석에서 우리는 제약 공간에서의 다이나믹스가 대략 | 앞서 분석에서 우리는 제약 공간에서의 다이나믹스가 대략 | ||
* a1 + d * (b v + k r) = (1 - d) * a0 | * a1 + d * (b v + k r) = (1 - d) * a0 | ||
* 가속도 + 상수 * (단단함 * 속도 + 댐핑 * 위치) = (1 - 상수) * 원래 가속도 | * 가속도 + 상수 * (단단함 * 속도 + 댐핑 * 위치) = (1 - 상수) * 원래 가속도 | ||
으로 나타냄을 밝혔다. | 으로 나타냄을 밝혔다. | ||
| 42번째 줄: | 56번째 줄: | ||
===solimp: real(5), "0.9 0.95 0.001 0.5 2"=== | === solimp: real(5), "0.9 0.95 0.001 0.5 2" === | ||
다섯 개의 숫자는 (dmin, dmax, width, midpoint, power)이다. 이것은 함수 d(r)의 파라미터를 결정한다. (최소 d, 최대 d, 너비, 중간점, 차수) | 다섯 개의 숫자는 (dmin, dmax, width, midpoint, power)이다. 이것은 함수 d(r)의 파라미터를 결정한다. (최소 d, 최대 d, 너비, 중간점, 차수) | ||
| 60번째 줄: | 74번째 줄: | ||
** 참고로 차수가 1이면, 함수는 중간점과 관계 없는 선형이 된다. | ** 참고로 차수가 1이면, 함수는 중간점과 관계 없는 선형이 된다. | ||
[[파일: | [[파일:Mj_impedance.png|500x500픽셀]] | ||
이 그림은 가로 축의 r의 제약 위반에 대한 세로 축의 응답 d(r)를 보인다. | 이 그림은 가로 축의 r의 제약 위반에 대한 세로 축의 응답 d(r)를 보인다. | ||
| 83번째 줄: | 97번째 줄: | ||
===solref: real(2), "0.02 1"=== | === solref: real(2), "0.02 1" === | ||
이 속성은 숫자의 부호에 의해 두 가지의 형식으로 결정된다. | 이 속성은 숫자의 부호에 의해 두 가지의 형식으로 결정된다. | ||
| 113번째 줄: | 127번째 줄: | ||
*** 댐핑 = 단단함 / (최대 d의 제곱) | *** 댐핑 = 단단함 / (최대 d의 제곱) | ||
==액추에이터 길이 범위 (Actuator length range)== | == 액추에이터 길이 범위 (Actuator length range) == | ||
MuJoCo 2.0에서, mjModel.actuator_lengthrange 필드는 액추에이터의 구동 가능한 길이의 범위를 담고 있다 (혹은 더 정확하게, 액추에이터의 전달 가능 범위). | MuJoCo 2.0에서, mjModel.actuator_lengthrange 필드는 액추에이터의 구동 가능한 길이의 범위를 담고 있다 (혹은 더 정확하게, 액추에이터의 전달 가능 범위). | ||
| 128번째 줄: | 142번째 줄: | ||
이 범위를 정하기 위한 방법은 세 가지가 있다: | 이 범위를 정하기 위한 방법은 세 가지가 있다: | ||
* 모든 액추에이터에 새로운 속성값인 lengthrange 값을 명시적으로 제공한다. | * 모든 액추에이터에 새로운 속성값인 lengthrange 값을 명시적으로 제공한다. | ||
* 액추에이터가 붙어 있는 joint나 tendon의 제한값으로부터 복사 해 온다. | * 액추에이터가 붙어 있는 joint나 tendon의 제한값으로부터 복사 해 온다. | ||
| 141번째 줄: | 156번째 줄: | ||
자동 계산은 수정된 물리 시뮬레이션에 의존한다. | 자동 계산은 수정된 물리 시뮬레이션에 의존한다. | ||
* 각각의 액추에이터에 대해서 우리는 힘(최소 길이를 계산할 때 음의 힘, 최대 길이를 계산할 때 양의 힘)을 액추에이터의 전달 가능 범위에 대해 적용하고, | * 각각의 액추에이터에 대해서 우리는 힘(최소 길이를 계산할 때 음의 힘, 최대 길이를 계산할 때 양의 힘)을 액추에이터의 전달 가능 범위에 대해 적용하고, | ||
* 시뮬레이션의 불안정성을 피하기 위해 댐핑된 환경 하에서 시뮬레이션을 진행하며, | * 시뮬레이션의 불안정성을 피하기 위해 댐핑된 환경 하에서 시뮬레이션을 진행하며, | ||
| 165번째 줄: | 181번째 줄: | ||
후자(기하학)를 설명하기 위해, 한 쪽은 world에, 다른 한 쪽은 world에 붙어 있는 힌지 관절 주변으로 회전하는 물체에 매달려 있는 tendon을 생각해보자. | 후자(기하학)를 설명하기 위해, 한 쪽은 world에, 다른 한 쪽은 world에 붙어 있는 힌지 관절 주변으로 회전하는 물체에 매달려 있는 tendon을 생각해보자. | ||
* 이 경우 tendon의 최소 및 최대 길이는 잘 정의된다. | * 이 경우 tendon의 최소 및 최대 길이는 잘 정의된다. | ||
** 공간에서 부착 점의 궤도가 그리는 원의 크기에 의존된다. | ** 공간에서 부착 점의 궤도가 그리는 원의 크기에 의존된다. | ||
| 179번째 줄: | 196번째 줄: | ||
만약 어떤 모델에서 수렴 에러가 발생한다면, 아마 그 이유는 모델에 관절 제한을 넣는 것을 깜빡 했었을 것이다. | 만약 어떤 모델에서 수렴 에러가 발생한다면, 아마 그 이유는 모델에 관절 제한을 넣는 것을 깜빡 했었을 것이다. | ||
==근육 액추에이터 (Muscle Actuators)== | == 근육 액추에이터 (Muscle Actuators) == | ||
MuJoCo 2.0에서, 우리는 생물학적 근육을 모델링하기 위한 도구를 제공한다. 최소한의 노력으로 근육을 추가하고 싶은 사용자는 액추에이터 섹션에 한 줄의 XML으로 구현할 수 있다. | MuJoCo 2.0에서, 우리는 생물학적 근육을 모델링하기 위한 도구를 제공한다. 최소한의 노력으로 근육을 추가하고 싶은 사용자는 액추에이터 섹션에 한 줄의 XML으로 구현할 수 있다. | ||
| 212번째 줄: | 229번째 줄: | ||
따라서 MuJoCo에서의 tendon 길이는, 생체역학에서의 근육+tendon 길이와 같다. | 따라서 MuJoCo에서의 tendon 길이는, 생체역학에서의 근육+tendon 길이와 같다. | ||
* 여기서는 생물학적 tendon이 상수 길이 LT로 딱딱하게 고정되어 있다고 가정하고, 생물학적 근육 길이 LM은 시간에 따라 변한다고 취급한다. | * 여기서는 생물학적 tendon이 상수 길이 LT로 딱딱하게 고정되어 있다고 가정하고, 생물학적 근육 길이 LM은 시간에 따라 변한다고 취급한다. | ||
* 따라서 MuJoCo의 tendon 길이는, 생물학적 tendon과 근육 길이의 합이다: | * 따라서 MuJoCo의 tendon 길이는, 생물학적 tendon과 근육 길이의 합이다: | ||
| 219번째 줄: | 237번째 줄: | ||
또 다른 중요한 상수는 근육의 휴식기 최적 길이(L0)이다. | 또 다른 중요한 상수는 근육의 휴식기 최적 길이(L0)이다. | ||
* 이는 근육이 속도가 0일 때, 동적 힘(active force)을 최대로 생성할 때의 근육 길이 LM이다. | * 이는 근육이 속도가 0일 때, 동적 힘(active force)을 최대로 생성할 때의 근육 길이 LM이다. | ||
우리는 사용자에게 L0과 LT를 직접 묻지 않는다. | 우리는 사용자에게 L0과 LT를 직접 묻지 않는다. | ||
* 왜냐하면 공간적 복잡성한 tendon의 경로 및 감쌈(wrapping) 조건 하에서 이 값들을 알아내는 것이 어렵기 때문이다. | * 왜냐하면 공간적 복잡성한 tendon의 경로 및 감쌈(wrapping) 조건 하에서 이 값들을 알아내는 것이 어렵기 때문이다. | ||
* 대신 우리는 아래와 같이 L0과 LT를 계산한다. | * 대신 우리는 아래와 같이 L0과 LT를 계산한다. | ||
| 236번째 줄: | 256번째 줄: | ||
실행 시간에, 우리는 스케일 된 근육 길이와 속도를 다음과 같이 계산한다: | 실행 시간에, 우리는 스케일 된 근육 길이와 속도를 다음과 같이 계산한다: | ||
* L = (actuator_length - LT) / L0 | * L = (actuator_length - LT) / L0 | ||
** L = LM / L0 | ** L = LM / L0 | ||
| 244번째 줄: | 265번째 줄: | ||
많은 실험 논문들에서 측정한 힘-길이-속도(Force-Length-Velocity, FLV) 함수에 의해 행동이 결정된다. 우리는 이 함수를 다음과 같이 근사한다: | 많은 실험 논문들에서 측정한 힘-길이-속도(Force-Length-Velocity, FLV) 함수에 의해 행동이 결정된다. 우리는 이 함수를 다음과 같이 근사한다: | ||
[[파일: | [[파일:Mujoco_Musclemodel.png|500x500픽셀]] | ||
함수는 다음과 같이 구성된다. | 함수는 다음과 같이 구성된다. | ||
* FLV(L, V, act) = FL(L)*FV(V)*act + FP(L) | * FLV(L, V, act) = FL(L)*FV(V)*act + FP(L) | ||
** FLV = (동적힘)길이 함수 * (동적힘)속도 함수 * 활성화도 + (정적힘)길이 함수 | ** FLV = (동적힘)길이 함수 * (동적힘)속도 함수 * 활성화도 + (정적힘)길이 함수 | ||
* MuJoCo 액추에이터의 일반적인 형태와 비교해 보면, FL*FV를 액추에이터 이득(gain)으로, FP를 액추에이터 편향(bias)로 볼 수 있다. | * MuJoCo 액추에이터의 일반적인 형태와 비교해 보면, FL*FV를 액추에이터 이득(gain)으로, FP를 액추에이터 편향(bias)로 볼 수 있다. | ||
* FL은 길이에 대한 동적 힘이다. | * FL은 길이에 대한 동적 힘이다. | ||
* FV는 속도에 대한 동적 힘이다. | * FV는 속도에 대한 동적 힘이다. | ||
* 이들은 전체 동적 힘을 계산하기 위해 곱해진다(참고로 액추에이션 활성화도인 act에 의해 스케일링된다). | * 이들은 전체 동적 힘을 계산하기 위해 곱해진다(참고로 액추에이션 활성화도인 act에 의해 스케일링된다). | ||
* FP는 활성화도와 관계 없이 항상 존재하는 정적 힘이다. | * FP는 활성화도와 관계 없이 항상 존재하는 정적 힘이다. | ||
| 258번째 줄: | 280번째 줄: | ||
우리는 스케일 된 근육의 힘에 근육에 관한 상수 F0를 곱해 실제 힘을 얻는다: | 우리는 스케일 된 근육의 힘에 근육에 관한 상수 F0를 곱해 실제 힘을 얻는다: | ||
* actuator_force = -1 * FLV(L, V, act) * F0 | * actuator_force = -1 * FLV(L, V, act) * F0 | ||
* 음수 부호가 붙는 이유는 양의 활성화도는 근육의 당기는 힘을 생성하기 때문이다. (역주: 양수이면 물체를 밀어내고, 음수이면 물체를 당겨온다) | * 음수 부호가 붙는 이유는 양의 활성화도는 근육의 당기는 힘을 생성하기 때문이다. (역주: 양수이면 물체를 밀어내고, 음수이면 물체를 당겨온다) | ||
| 274번째 줄: | 297번째 줄: | ||
게다가, FLV 함수 자체 또한 여러 파라미터를 갖고 있다: lmin, lmax, vmax, fpmax, fvmax. | 게다가, FLV 함수 자체 또한 여러 파라미터를 갖고 있다: lmin, lmax, vmax, fpmax, fvmax. | ||
* 이 5가지 값들은 모든 근육에 대해 동일할 것이라 예상된다. | * 이 5가지 값들은 모든 근육에 대해 동일할 것이라 예상된다. | ||
* 하지만 여러 다른 실험 논문들에서 다른 형태의 FLV 함수 형태를 제안하므로, 사용자가 그 논문에 익숙하다면 거기에 맞게 파라미터를 조정하고 싶을 것이다. | * 하지만 여러 다른 실험 논문들에서 다른 형태의 FLV 함수 형태를 제안하므로, 사용자가 그 논문에 익숙하다면 거기에 맞게 파라미터를 조정하고 싶을 것이다. | ||
| 282번째 줄: | 306번째 줄: | ||
아래가 이를 묘사하는 그림이다. | 아래가 이를 묘사하는 그림이다. | ||
[[파일: | [[파일:Mj_musclerange.png|500x500픽셀]] | ||
정규화된 FL 곡선에 각 근육의 가용 범위를 겹쳐 놓은 이 그림은 생체역학적 논문에서 흔한 형태이다 (수직 변위는 무시). | 정규화된 FL 곡선에 각 근육의 가용 범위를 겹쳐 놓은 이 그림은 생체역학적 논문에서 흔한 형태이다 (수직 변위는 무시). | ||
| 332번째 줄: | 356번째 줄: | ||
** 우리의 근육 모델의 파라미터를 바꾸는 대신, general 액추에이터의 gaintype, biastype, dyntype을 "user"로 바꾸고 실행 시간에 콜백을 제공함으로서 사용자는 다른 모델을 구현할 수 있다. 아니면, 이 타입 중에 일부는 "muscle"로 남겨 두어 우리 모델을 쓰고, 다른 요소만 교체할 수 있다. 참고로 tendon 기하학적 계산은 여전히 표준 MuJoCo 파이프라인에 의해 관리되어 사용자의 근육 모델에 actuator_length, actuator_velocity, actuator_lengthrange를 입력으로서 제공한다. 사용자 콜백은 부드러운 tendon의 모델링 등 우리가 무시하기로 한 기타 상세한 사항을 시뮬레이트하는데 쓰일 수 있다. | ** 우리의 근육 모델의 파라미터를 바꾸는 대신, general 액추에이터의 gaintype, biastype, dyntype을 "user"로 바꾸고 실행 시간에 콜백을 제공함으로서 사용자는 다른 모델을 구현할 수 있다. 아니면, 이 타입 중에 일부는 "muscle"로 남겨 두어 우리 모델을 쓰고, 다른 요소만 교체할 수 있다. 참고로 tendon 기하학적 계산은 여전히 표준 MuJoCo 파이프라인에 의해 관리되어 사용자의 근육 모델에 actuator_length, actuator_velocity, actuator_lengthrange를 입력으로서 제공한다. 사용자 콜백은 부드러운 tendon의 모델링 등 우리가 무시하기로 한 기타 상세한 사항을 시뮬레이트하는데 쓰일 수 있다. | ||
===OpenSim과의 관계성=== | === OpenSim과의 관계성 === | ||
생체역학계의 연구자들이 사용하는 표준 소프트웨어는 OpenSim이다. 우리는 우리의 근육 모델을 훨씬 더 빠르고 안정적인 시뮬레이션을 하기 위해 조금 단순화하였지만, 그래도 가능한 OpenSim 모델과 비슷하도록 설계했다. MuJoCo 사용자가 OpenSim 모델을 변환하는 것을 돕기 위해, 우리는 비슷한 점과 차이점을 정리했다. | 생체역학계의 연구자들이 사용하는 표준 소프트웨어는 OpenSim이다. 우리는 우리의 근육 모델을 훨씬 더 빠르고 안정적인 시뮬레이션을 하기 위해 조금 단순화하였지만, 그래도 가능한 OpenSim 모델과 비슷하도록 설계했다. MuJoCo 사용자가 OpenSim 모델을 변환하는 것을 돕기 위해, 우리는 비슷한 점과 차이점을 정리했다. | ||
| 370번째 줄: | 394번째 줄: | ||
참고로 래핑된 tendon의 곡선 부분은 직선으로 렌더링되지만, 기하학적 파이프라인은 실제 곡선에 맞게 동작하며, 그들의 길이와 모멘트를 해석적으로 계산한다. | 참고로 래핑된 tendon의 곡선 부분은 직선으로 렌더링되지만, 기하학적 파이프라인은 실제 곡선에 맞게 동작하며, 그들의 길이와 모멘트를 해석적으로 계산한다. | ||
[[파일: | [[파일:Mj_tendonwraps.png|500x500픽셀]] | ||
=XML 문서 (XML Reference)= | = XML 문서 (XML Reference) = | ||
===actuator/muscle=== | === actuator/muscle === | ||
이 요소는 근육 액추에이터 섹션에서 설명한 대로 근육 액추에이터를 모델링하기 위해 사용된다. | 이 요소는 근육 액추에이터 섹션에서 설명한 대로 근육 액추에이터를 모델링하기 위해 사용된다. | ||
* name: string, optional | * name: string, optional | ||
** 요소 이름. 이름 요소 섹션 참고. | ** 요소 이름. 이름 요소 섹션 참고. | ||
| 383번째 줄: | 408번째 줄: | ||
** 액추에이터가 속할 정수 그룹. 이 요소는 커스텀 태그로 사용될 수 있다. 또한 visualizer에서 그룹별 액추에이터 렌더링 활성화/비활성화에도 쓰인다. | ** 액추에이터가 속할 정수 그룹. 이 요소는 커스텀 태그로 사용될 수 있다. 또한 visualizer에서 그룹별 액추에이터 렌더링 활성화/비활성화에도 쓰인다. | ||
* ctrllimited : [false, true], "false" | * ctrllimited : [false, true], "false" | ||
** true: 이 액추에이터로의 제어 입력은 실행 시간에 ctrlrange 대로 클램핑된다. | ** true: 이 액추에이터로의 제어 입력은 실행 시간에 ctrlrange 대로 클램핑된다. | ||
** false: 클램핑 비활성화 | ** false: 클램핑 비활성화 | ||
** 참고로 option flag의 clampctrl 속성으로 제어 입력 클램핑을 전역 비활성화 할 수 있다. | ** 참고로 option flag의 clampctrl 속성으로 제어 입력 클램핑을 전역 비활성화 할 수 있다. | ||
| 420번째 줄: | 445번째 줄: | ||
* fvmax : real, "1.2" | * fvmax : real, "1.2" | ||
** 포화 수축 속도일때 생성되는 동적 힘. 휴식기 최대 힘과 관련이 있다. | ** 포화 수축 속도일때 생성되는 동적 힘. 휴식기 최대 힘과 관련이 있다. | ||
== 그래서 range, lengthrange 등은 뭐가 다른거냐고? == | |||
=== tendon === | |||
* range: tendon의 물리적인 길이 제한. 이 길이 이상으로는 '''절대로''' 늘어날 수 없다. | |||
=== muscle === | |||
* lengthrange: muscle의 가동 범위. tendon의 range와는 다르게, 이 근육이 '''물리 시뮬레이션의 제약을 바탕으로 최대로 늘어날 수 있는 길이'''를 줘야 한다. (팔에 달린 근육은, 팔의 관절 각도 이상으로 늘어날 수 없다.) | |||
* range: L0 단위로 정의된 근육의 동작 범위. '''근육 힘 특성인 L0과 LT의 계산을 위해 쓰인다.''' | |||
2021년 11월 8일 (월) 09:37 기준 최신판
참고: 아래의 모든 내용은 mujoco.org/book 을 비공식적으로 번역한 것이며, 오역이 있을 수 있습니다. 문제시 삭제하겠습니다. DISCLAIMER: This is an unofficial translation of mujoco.org/book and may be mistranslated. Will be removed if any problem.
계산 (Computation)
파라미터 (Parameters)
= 제약 집합
여기서 가 모델 파라미터로부터 어떻게 계산되는지 설명한다. 선택된 파라미터화가 make sense하기 위하여, 우리는 먼저 이 수치들이 어떻게 다이나믹스에 영향을 미치는지 이해해야 한다. 우리는 (4)의 제약되지 않은 minimizer,
다음으로 참조(reference) 가속도의 계산 방법을 설명한다. 이미 언급한 바와 같이, damping(감쇠) 및 stiffness(강성) 계수에 의해 매개 변수화된 스프링 댐퍼 모델을 요소별로 사용한다:
요약하면, 사용자는 임피던스 계수 , damping 계수 과 stiffness 계수 들의 벡터를 지정한다. 그 뒤 위와 같이 는 MuJoCo에 의해 계산되고, 선택된 최적화 알고리즘이 문제 (4)를 풀기 위해 적용된다. Modeling 챕터의 Solver parameters 섹션에서 설명하듯이, MuJoCo는 임계 damping에 도달하도록 설정을 위한 추가적인 자동화를 제공하거나, 거리에 따라 바뀌는 를 통한 부드러운 contact 레이어를 제공한다.
모델링 (Modeling)
Solver 파라미터 (Solver parameters)
Computation 챕터의 Solver 파라미터 섹션에서 MuJoCo의 제약의 행동을 결정하는 수치 d, b, k의 수학적 알고리즘적 의미를 설명했다. 여기서 우리는 그것을 어떻게 설정하는지 설명한다.
설정은 '제약'을 갖고 있는 모든 MJCF 요소의 solref와 solimp attribute에 의해 간접적으로 완료된다.
이 파라미터들은 각 제약 또는 각 기본 클래스에 대해 조정되거나, 혹은 미설정 상태로 남겨둘 수 있다 - 그러면 MuJoCo는 아래에 나와 있는 내부 기본 값을 사용한다.
참고로 option에서 오버라이드 메커니즘도 가능하다; 런타임에 모든 접촉과 관련된 solver 파라미터를 바꾸는데 사용될 수 있어, 파라미터 세팅이나 수치 최적화에서의 연속적인 방법을 동적으로 실험할 수 있다.
여기서 우리는 한 개의 스칼라 제약에 초점을 둔다.
Computation 챕터에서와 조금 다른 표기법을 사용하여,
- a1을 가속도,
- v를 속도,
- r을 위치 또는 유수 (마찰 차원에서 0으로 정의된다),
- b와 k는 각각 스프링에서의 참조 가속도 aref = -b*v - k*r을 나타내기 위한 단단함, 댐핑을 나타낸다.
- d는 상수 응답(임피던스),
- a0은 제약 힘이 없을 때의 가속도라고 한다. (원래 가속도)
앞서 분석에서 우리는 제약 공간에서의 다이나믹스가 대략
- a1 + d * (b v + k r) = (1 - d) * a0
- 가속도 + 상수 * (단단함 * 속도 + 댐핑 * 위치) = (1 - 상수) * 원래 가속도
으로 나타냄을 밝혔다.
다시, 유저가 조정할 수 있는 파라미터는 d, b, k(상수, 단단함, 댐핑) 이다. 나머지 양들은 시스템의 상태이며 각 시간 스텝에서 자동으로 계산된다.
먼저 우리는 응답 상수 d에 대해 설명한다.
- d는 반드시 0~1 사이여야 한다; 내부적으로 MuJoCo는 0.0001 ~ 0.9999로 자른다.
- 이것이 solver가 a0과 aref 사이를 상호작용 할 수 있게 해준다.
- 작은 d값은 부드럽고 약한 제약이고, 큰 d값은 강하고 딱딱한 제약이다.
- 유저는 d를 상수로 설정하거나, 아니면 위치 의존적인 함수 d(r)로 설정할 수 있다.
- 위치 의존적 응답은 물체 주변의 부드러운 접촉 레이어로 사용하거나, 혹은 큰 위반일수록 강해지는 equality 제약을 정의할 수 있다. (따라서 예제에서의 backlash를 근사할 수 있다)
- 함수 d(r)의 모양은 요소별로 정의할 수 있는 solimp 벡터 파라미터로 정의할 수 있다.
solimp: real(5), "0.9 0.95 0.001 0.5 2"
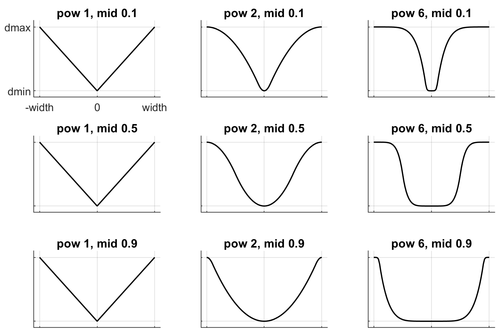
다섯 개의 숫자는 (dmin, dmax, width, midpoint, power)이다. 이것은 함수 d(r)의 파라미터를 결정한다. (최소 d, 최대 d, 너비, 중간점, 차수)
MuJoCo 2.0 이전에서는 3개였으며, 거기에 함수의 형태를 결정하는 한 개의 추가 전역 옵션이 있었다.
MuJoCo 2.0에서는 이전 버전의 호환성을 유지하며 응답 함수를 확장했다.
이전 버전에서 앞의 3개만 설정 가능했고, 기본값은 똑같다.
뒤의 2개의 기본값은 이전 버전과 똑같은 함수의 모양 (시그모이드)를 생성한다.
- 새롭게 정의된 뒤의 2개는 함수의 이동(shift)나 조여짐(skew)을 조정할 수 있다.
- 아래 그림은 사실은 두 반사된 시그모이드(???)를 보여주고 있으며, 이는 응답 함수 d(r)이 r의 절대값에 의존하기 때문이다.
- 이 유연성은 원격 접촉 힘에 대한 더 나은 조절을 하기 위해 추가되었으며, 또한 다른 제약을 위해서도 사용될 수 있다.
- (함수를 생성하기 위한 다항 스플라인의) 차수는 1과 같거나 커야한다.
- (반사 지점을 결정하는) 중간점은 0과 1 사이여야 하고, 단위는 너비이다.
- 참고로 차수가 1이면, 함수는 중간점과 관계 없는 선형이 된다.
이 그림은 가로 축의 r의 제약 위반에 대한 세로 축의 응답 d(r)를 보인다.
- equality 제약에 대해서는, r은 제약 위반과 같다 (양수 또는 음수 가능).
- 마찰 손실 또는 타원뿔의 마찰 차원에 대해서는, r은 항상 0이다.
- 제한(limit), 타원뿔의 법선 방향, 사각뿔의 모든 법선 방향에 대해서는 r은 (제약 또는 접촉) 거리에서 제약이 활성화 되는 margin을 뺀 값이다; 접촉에 대해서 이 margin은 실제로 margin-gap이다.
- 따라서 제한과 접촉 제약은 r이 음수일 때 활성화된다.
다음은 단단함 k와 댐핑 b에 대해 설명한다.
여기에서의 아이디어는 위의 질량-스프링-댐퍼 시스템에서의 시상수와 댐핑 비율에 대한 파라미터의 재조정이다.
"시상수"에 의해 우리는 자연 주파수 / 댐핑 비율 의 평균을 구한다 (???)
1차 다이나믹스를 가진 유수가 0인 제약이나 질량-스프링-댐퍼 분석은 적용하지 않는다 (???)
그런 경우에는 시상수는 등속의 지수 감쇠에 대한 rate 이며 (???) 댐핑 비율은 무시된다.
이 형식에서, MuJoCo 2.0은 단단함과 댐핑을 더 직접적으로 정의할 수 있는 2차 형식을 제공한다. (???)
solref: real(2), "0.02 1"
이 속성은 숫자의 부호에 의해 두 가지의 형식으로 결정된다.
- 두 숫자가 둘 다 양수이면 (timeconst, dampratio) = (시상수, 댐핑 비율)로 결정된다.
- 모든 MuJoCo에서 가능하다.
- 이 경우 우리는 적절한 스케일링 후 k, b를 계산하기 위해 질량-스프링-댐퍼 모델을 쓴다.
- 참고로 활성화된 (effective) 단단함 d(r)*k와 댐핑 d(r)*b는 거리 r에 대한 함수인 응답 d(r)에 의해 스케일 된다.
- 따라서 우리는 d에 대한 스케일링을 완전히 되돌리기 전까지는 지정된 질량-스프링-댐퍼 속성을 항상 만족할 수는 없다. (???)
- 하지만 스케일링을 완전히 되돌리는 것은 원하지 않을 것인데, 왜냐하면 그것은 상호작용 속성을 파괴할 것이고, 특히 제한 d=0이 더 이상 제약을 비활성화 하지 않는다.
- 대신에 우리는 단단함과 댐핑을 스케일하여, 댐핑 비율을 상수로 유지하고, d(r)이 작아짐에 따라 시상수를 증가시킨다.
- 스케일링 수식은
- b = 2 / (dmax * timeconst)
- 단단함 = 2 / (최대 d * 시상수)
- k = d(r) / (dmax * dmax * timeconst * timeconst * dampratio * dampratio)
- 댐핑 = d의 함수 / (최대 d의 제곱 * 시상수의 제곱 * 댐핑 비율의 제곱)
- 시상수 파라미터는 시뮬레이션 타임 스텝보다 최소 2배 이상 커야 한다.
- 아니면 시스템은 산술 integrator에 대해 너무 단단할 것이고 (특히 오일러 integration) 불안정할 것이다.
- 이건 내부적으로 지켜지며, refsafe를 false로 하면 무시할 수 있다.
- 댐핑 비율 파라미터는 보통 1로 설정한다. (치명적 댐핑???)
- 작은 값은 under-댐핑 또는 통통 튀는 제약이 될 것이고, 큰 값은 over-댐핑되는 제약이 될 것이다.
- 그 외는 (-stiffness, -damping) = (-단단함, -댐핑)으로 결정된다.
- MuJoCo 2.0에서 도입되었다.
- 이 것은 원상 회복(???, restitution)에 대한 더욱 직접적인 조정을 가능하게 한다.
- 우리는 여전히 조금 스케일링을 적용하므로 같은 숫자들이 다른 응답들에 대해 사용될 수 있지만, 더 이상 스케일링이 r에 의존하지 않고 두 숫자는 더 이상 상호작용하지 않는다.
- 스케일링 수식은
- b = damping / dmax
- 단단함 = 댐핑 / 최대 d
- k = stiffness / (dmax * dmax)
- 댐핑 = 단단함 / (최대 d의 제곱)
액추에이터 길이 범위 (Actuator length range)
MuJoCo 2.0에서, mjModel.actuator_lengthrange 필드는 액추에이터의 구동 가능한 길이의 범위를 담고 있다 (혹은 더 정확하게, 액추에이터의 전달 가능 범위).
이것은 밑에서 설명할 근육 액추에이터 시뮬레이션에 필요하다. 여기서는 actuator_lengthrange의 의미 및 설정법에 촛점을 맞춘다.
정확한 물리적 혹은 기하학적 양인 mjModel의 다른 필드와는 다르게, actuator_lengthrange는 추정값이다.
이 값은 직관적으로 생각하면 모델의 모든 "구동 가능한" 조합들에 대해서의 액추에이터의 전달력이 도달할 수 있는 길이를 의미한다.
하지만 MuJoCo의 제약은 soft 방식이므로, 원칙상 어떤 조합도 구동 가능하다고 할 수 있다.
이와 동시에 우리는 근육 모델링을 위해 잘 정의된 범위도 필요하다.
이 범위를 정하기 위한 방법은 세 가지가 있다:
- 모든 액추에이터에 새로운 속성값인 lengthrange 값을 명시적으로 제공한다.
- 액추에이터가 붙어 있는 joint나 tendon의 제한값으로부터 복사 해 온다.
- 아래에서 설명하는 대로, 자동으로 계산한다. 이 계산에는 많은 옵션들이 있고, XML option 노드의 lengthrange에서 설정 가능하다.
액추에이터 길이 범위의 자동 계산은 컴파일 시간에 완료되고, 결과는 컴파일 된 모델의 mjModel.actuator_lengthrange에 저장된다.
이 후 모델이 저장되면 (XML이나 MJB로), 다음 번 로딩에서 재계산이 필요 없다. 대규모 근골격 모델을 로드 할 때 컴파일러에서의 계산이 느려질 수 있기 때문에, 이 처리는 중요하다.
이 계산만을 위해 컴파일러의 멀티스레딩 구현을 하였다(각각의 액추에이터에 대해 여러 스레드에서 병렬 처리). 이는 MuJoCo 라이브러리를 리눅스나 macOS에서 링크할 때 '-pthread' 플래그가 필요하게 된 이유이다.
자동 계산은 수정된 물리 시뮬레이션에 의존한다.
- 각각의 액추에이터에 대해서 우리는 힘(최소 길이를 계산할 때 음의 힘, 최대 길이를 계산할 때 양의 힘)을 액추에이터의 전달 가능 범위에 대해 적용하고,
- 시뮬레이션의 불안정성을 피하기 위해 댐핑된 환경 하에서 시뮬레이션을 진행하며,
- 안정될 때까지 충분한 시간을 주고, 결과를 기록한다.
이는 모멘텀 하에서의 경사 하강법과 비슷하다. 실제로 우리는 명시적 경사(그라디언트) 기반 최적화 기법으로 실험도 해 보았지만, (주어진 여러 soft 제약 하에서) 무엇을 최적화 해야 하는지 명확하지 않다는 문제가 있었다.
시뮬레이션을 사용하여, 우리는 본질적으로 물리 환경이 우리에게 무엇을 최적화해야 하는지 말하도록 한다.
염두에 두어야 할 것은, 이것은 여전히 최적화 프로세스이며, 아마도 계산된 파라미터를 재조정 할 필요도 있을 것이다.
우리는 대부분의 모델에서 동작할 보수적인 기본값을 제공하지만, 동작하지 않을 경우, 미세 조정을 위해 lengthrange 속성값을 이용하면 된다.
이 기능을 사용 할 때 모델의 기하학(geometry)를 염두에 두는 것이 중요하다.
여기에서의 암묵적 가정은 구동 가능한 액추에이터의 길이는 제한되어 있다는 것이다.
게다가 우리는 접촉을 제한 요소로서 고려하지 않는다 (사실 우리는 이 시뮬레이션에서 접촉을 비롯해 정적(passive) 힘, 중력, 마찰 손실, 액추에이터 힘을 내부적으로 비활성화시킨다).
그 이유는 접촉이 있는 모델은 얽힐 수 있고 많은 지역 최적해를 만들 수 있기 때문이다.
따라서 액추에이터는 모델에 정의되어 있는 (이 시뮬레이션에서 활성화 되어 있는)관절 혹은 tendon의 제한, 또는 기하학(geometry)에 의해 제한되어야 한다.
후자(기하학)를 설명하기 위해, 한 쪽은 world에, 다른 한 쪽은 world에 붙어 있는 힌지 관절 주변으로 회전하는 물체에 매달려 있는 tendon을 생각해보자.
- 이 경우 tendon의 최소 및 최대 길이는 잘 정의된다.
- 공간에서 부착 점의 궤도가 그리는 원의 크기에 의존된다.
- 사용자에 의해 정의된 관절이나 tendon에 길이 제한이 없음에도 불구하고 말이다.
그러나 만약 액추에이터가 관절 혹은 관절과 equal한 tendon 그 자체에 부착되어 있다면, 제한이 없어지게 된다.
이런 경우는 컴파일러가 에러를 내지만, 에러의 이유가 길이가 수렴하지 않아서인지 아니면 액추에이터 길이가 무제한인지 말해줄 수는 없다.
이 내용들은 너무 복잡하게 들리는데, 우리가 가능한 매우 특이한 경우를 설명하고 있기 때문이다.
실제로(현실적으로)는 길이 범위는 거의 모든 경우에 spatial tendon에 붙은 근육 액추에이터에서 사용될 것이며, 또한 아마도 모델의 관절 제한이 있을 것이기 때문에, 효과적으로 근육 액추에이터의 길이를 잘 제한시킬 것이다.
만약 어떤 모델에서 수렴 에러가 발생한다면, 아마 그 이유는 모델에 관절 제한을 넣는 것을 깜빡 했었을 것이다.
근육 액추에이터 (Muscle Actuators)
MuJoCo 2.0에서, 우리는 생물학적 근육을 모델링하기 위한 도구를 제공한다. 최소한의 노력으로 근육을 추가하고 싶은 사용자는 액추에이터 섹션에 한 줄의 XML으로 구현할 수 있다.
<actuator>
<muscle name="mymuscle" tendon="mytendon">
</actuator>
생물학적 근육은 서로 매우 달라 보이지만, 신기하게도 어떤 스케일링을 적용하면 전부 비슷한 형태로 움직인다. 우리의 기본 세팅은 그 스케일링을 적용하므로, 사용자는 파라미터 조정 없이도 쓸만한 근육 모델을 획득할 수 있다.
당연히 더 상세한 모델은 이 섹션에서 설명할 파라미터들의 조정이 필요하다.
근육 모델이 꽤 정교하지만, 여전히 MuJoCo 액추에이터의 한 타입으로 존재하며 다른 모든 액추에이터와 같은 컨벤션을 따른다.
근육은 general을 사용하여 정의할 수 있지만, 단축어 muscle이 더욱 편리하다.
다른 모든 액추에이터와 같이, 힘 생성 메커니즘과 전달 등은 독립적으로 정의된다. 그렇긴 하지만, 근육은 tendon 또는 관절에 부착되었을 때에만 (생물학)물리학적 의미를 갖는다.
여기서는 tendon 에 부착되었다고 가정한다.
먼저 우리는 길이와 길이 스케일링에 대해 설명한다.
전달체 (예: MuJoCo tendon)의 구동 가능한 길이의 범위가 중요한 역할을 한다; 상단의 길이 범위 섹션을 참조하라.
- 생체역학에서, 근육과 tendon은 일렬로 연결되어 근육-tendon 액추에이터를 구성한다.
- MuJoCo에서는 이와 다르다
- 공간적(spatial) 속성 (특히 길이와 속도)를 가진 것이 tendon이고
- tendon을 당기는 추상적 힘 생성 메커니즘을 의미하는 것이 근육이다.
따라서 MuJoCo에서의 tendon 길이는, 생체역학에서의 근육+tendon 길이와 같다.
- 여기서는 생물학적 tendon이 상수 길이 LT로 딱딱하게 고정되어 있다고 가정하고, 생물학적 근육 길이 LM은 시간에 따라 변한다고 취급한다.
- 따라서 MuJoCo의 tendon 길이는, 생물학적 tendon과 근육 길이의 합이다:
- actuator_length = LT + LM
- 액추에이터 길이 = 생물학적 tendon 길이(LT) + 생물학적 근육 길이(LM)
또 다른 중요한 상수는 근육의 휴식기 최적 길이(L0)이다.
- 이는 근육이 속도가 0일 때, 동적 힘(active force)을 최대로 생성할 때의 근육 길이 LM이다.
우리는 사용자에게 L0과 LT를 직접 묻지 않는다.
- 왜냐하면 공간적 복잡성한 tendon의 경로 및 감쌈(wrapping) 조건 하에서 이 값들을 알아내는 것이 어렵기 때문이다.
- 대신 우리는 아래와 같이 L0과 LT를 계산한다.
- LT+LM(actuator_length)의 가용 범위는 계산은 위의 길이 범위 계산에서 언급했다.
- 여기에다가, 우리는 사용자에게 (여전히 모르는) 상수 L0으로 스케일 된 근육 길이 LM 의 가용 범위를 지정하도록 묻는다.
- 이것은 range 속성으로 정해지며, 기본 (스케일 된) 범위 값은 (0.75, 1.05) 이다.
- 이제 우리는 실제 및 스케일된 길이의 범위를 이용해서 두 상수 L0과 LT를 계산할 수 있다:
- (actuator_lengthrange[0] - LT) / L0 = range[0]
- (actuator_lengthrange[1] - LT) / L0 = range[1]
- (역주) 따라서 계산해 보면
- L0 = (actuator_lengthrange[1] - actuator_lengthrange[0]) / (range[1] - range[0])
- LT = ((actuator_lengthrange[0] * range[1]) - (actuator_lengthrange[1] * range[0])) / (range[1] - range[0])
실행 시간에, 우리는 스케일 된 근육 길이와 속도를 다음과 같이 계산한다:
- L = (actuator_length - LT) / L0
- L = LM / L0
- V = actuator_velocity / L0
스케일 된 양의 장점은 그 표현 상태에서는 모든 근육이 비슷하게 움직인다.
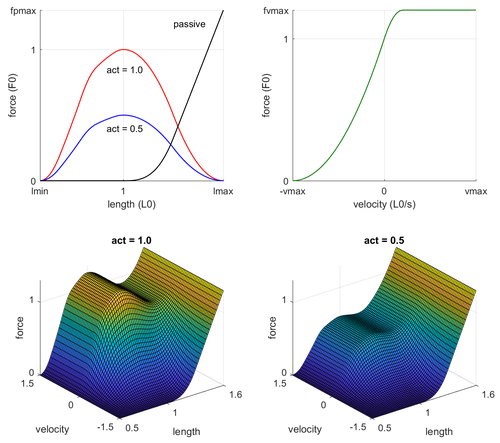
많은 실험 논문들에서 측정한 힘-길이-속도(Force-Length-Velocity, FLV) 함수에 의해 행동이 결정된다. 우리는 이 함수를 다음과 같이 근사한다:
함수는 다음과 같이 구성된다.
- FLV(L, V, act) = FL(L)*FV(V)*act + FP(L)
- FLV = (동적힘)길이 함수 * (동적힘)속도 함수 * 활성화도 + (정적힘)길이 함수
- MuJoCo 액추에이터의 일반적인 형태와 비교해 보면, FL*FV를 액추에이터 이득(gain)으로, FP를 액추에이터 편향(bias)로 볼 수 있다.
- FL은 길이에 대한 동적 힘이다.
- FV는 속도에 대한 동적 힘이다.
- 이들은 전체 동적 힘을 계산하기 위해 곱해진다(참고로 액추에이션 활성화도인 act에 의해 스케일링된다).
- FP는 활성화도와 관계 없이 항상 존재하는 정적 힘이다.
- FLV 함수의 출력은 스케일 된 근육의 힘이다.
우리는 스케일 된 근육의 힘에 근육에 관한 상수 F0를 곱해 실제 힘을 얻는다:
- actuator_force = -1 * FLV(L, V, act) * F0
- 음수 부호가 붙는 이유는 양의 활성화도는 근육의 당기는 힘을 생성하기 때문이다. (역주: 양수이면 물체를 밀어내고, 음수이면 물체를 당겨온다)
- 상수 F0는 속도가 0일 때, 동적 힘의 최대 값이다.
- 이는 근육의 두께와 상관이 있다. (예: 생리학적 단면적=PCSA)
- 값을 알고 있다면, muscle 요소의 force 속성으로 지정할 수 있다.
- 모른다면, 기본값인 -1로 지정해서, 밑에서 설명할 수식으로 계산하게 한다.
- 이 경우, 우리는 큰 근육일 수록 더 큰 무게를 움직이는 관절에 대해 작용한다는 사실에 따른다. force 속성을 다음과 같이 계산한다:
- F0 = scale / actuator_acc0
- actuator_acc0 값은 모델 컴파일러에 의해 사전 계산된다.
- 이는 액추에이터 전달에 대해 단위힘을 적용했을 때 발생하는 관절의 가속도의 norm이다.
- 직관적으로 scale의 의미는, 근육의 실제 강도는 전체 모델의 기하학적 및 관성적 속성에 의존하기는 하지만 근육이 "평균적"으로 얼마나 강한지를 결정하는 것이다.
우리는 지금까지 각각의 근육의 속성을 정의하는 3가지 상수를 마주했다: LT, L0, F0.
게다가, FLV 함수 자체 또한 여러 파라미터를 갖고 있다: lmin, lmax, vmax, fpmax, fvmax.
- 이 5가지 값들은 모든 근육에 대해 동일할 것이라 예상된다.
- 하지만 여러 다른 실험 논문들에서 다른 형태의 FLV 함수 형태를 제안하므로, 사용자가 그 논문에 익숙하다면 거기에 맞게 파라미터를 조정하고 싶을 것이다.
- 우리는 상단의 그림을 생성하고 우리가 어떻게 FLV 함수를 계산하는지 설명하는 MATLAB 함수 FLV.m 를 제공한다.
더욱 정확한 FLV 함수를 설계하는 미션에 착수하기 전에, FLV 함수의 형태보다는 근육의 (스케일된) 가용 범위 (역주: range 속성 (lmin, lmax, lengthrange가 아님))가 더 큰 영향을 미친다는 사실을 생각하는게 좋을 것이고, 많은 경우에 이 파라미터들은 알려져 있지 않다.
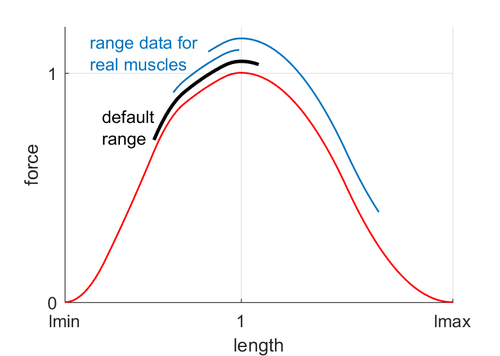
아래가 이를 묘사하는 그림이다.
정규화된 FL 곡선에 각 근육의 가용 범위를 겹쳐 놓은 이 그림은 생체역학적 논문에서 흔한 형태이다 (수직 변위는 무시).
우리의 기본 범위는 검정색으로 그려져 있다. 파란색 곡선은 두 팔 근육에 대한 실험 데이터이다.
작은 범위, 큰 범위, FL 곡선의 상승 부분에의 범위, 하강 부분에의 범위, 혹은 둘 다에의 범위 등에 걸쳐 있는 근육들을 볼 수 있다.
이제 50개의 근육을 갖고 있는 모델이 있다고 가정해보자. 정말 누군가가 너가 갖고 있는 그 모델의 모든 근육에 대한 작용 범위에 대해 그 근육이 뻗어 있는 관절들까지 생각해서 정성스럽게 실험하고 측정했을 것이라고 믿을 수 있나?
믿을 수 없다면, 그냥 생체 시스템처럼 근골격 모델은 동일한 일반적 행동을 보인다고 생각하는 게 나을 것이다 - 어떤 연구 커뮤니티들은 큰 관심을 갖고 있는 세부 사항까지 포함해서.
모델을 만든 사람이 상수(변하지 않는 수) 혹은 알려져 있다고 생각한 대부분의 근육 속성들에 대해서, 어떤 조건 하에서는 그 값들이 변하기도 한다는 것을 보이는 실험 논문들이 존재한다.
이것은 사람들이 정확한 모델을 만드는 용기를 잃게 하려는 게 아니라, 사람들이 그러한 모델에 대해 강한 신념을 가지지 못하게 하려는 것이다.
생물학계에서의 모델링은 물리학계 또는 공학계에서의 모델링과 매우 다르다... 이것이 로보틱스 하는 사람들이 정확한 로봇 모델을 만드는 것이 어렵다고 불평할 때 우리가 (속으로) 비꼬는 이유이다.
다시 우리 근육 모델의 근육 활성화도에 대한 얘기로 돌아오자. 이것은 입력이 제어 신호인 1차 비선형 필터의 상태이다. 필터 다이나믹스는 다음과 같다.
- d act / dt = (ctrl - act) / tau(ctrl, act)
- d 활성화도 / dt = (제어신호 - 활성화도) / tau(제어신호, 활성화도)
내부적으로 제어 신호는 액추에이터의 제어 범위가 지정되어 있지 않더라도 [0, 1]으로 클램프 된다.
여기에는 timeconst 속성으로 정의되는 두 개의 시상수가 있는데, timeconst = (tau_act, tau_deact)이고 기본 값은 (0.01, 0.04)이다. 실제 적용되는 시상수 tau는 다음과 같이 실행 시간에 결정된다.
- if ctrl > act
- tau(ctrl, act) = tau_act * (0.5 + 1.5*act)
- else
- tau(ctrl, act) = tau_deact / (0.5 + 1.5*act)
이제 우리는 muscle 요소에서 사용자가 그들의 익숙한 생체역학적 논문에 따르기 위해서 및 특정 모델에서의 더 정확한 측정값을 사용하여 조정하기 원할 것 같은 속성들을 정리한다.
- Defaults
- 모든 곳에서 기본 값을 사용한다. 해야할 일은 이 장의 처음에서 보인 것처럼 tendon에 근육을 붙이는 것 뿐이다. 이것만으로도 꽤나 적절한 모델을 만들 수 있다.
- scale
- 각 근육의 강도는 모르지만 모든 근육을 강하거나 약하게 하고 싶을 때, scale을 조정하면 된다. 이것은 각각의 근육에 다르게 조정할 수 있지만, default 요소로 한 번에 모든 근육을 바꾸는 것이 더 적절할 것이다.
- force
- 만약 각 근육의 최대 동적 힘 F0을 알고 있다면, 여기에 입력하면 된다. 많은 실험 논문들이 이 데이터를 갖고 있다.
- range
- 근육의 동작 범위는 스케일된 길이이고 어떤 논문들에는 이 값도 적혀 있다. 그 (수많은 관절에 대해 작용하는 특정 근육에 대한) 측정 값들을 얼마나 믿을 수 있는지는 둘째치고, 어쨌든 적혀 있다. 참고로 range는 각 근육마다 대체적으로 다르다.
- timeconst
- 근육은 천천히 경련하는 섬유와 빠르게 경련하는 섬유의 조합이다(slow/fast-twitch fibers). 표준 적인 근육은 섞여 있지만, 어떤 근육들은 각 섬유 타입에 대한 비율이 다르기도 하여, 근육이 더 빠르게/느리게 움직이게 한다. 이것은 시상수를 조정하여 모델링할 수 있다. FLV 함수의 vmax 파라미터도 같이 적절하게 조정해야 할 것이다.
- lmin, lmax, vmax, fpmax, fvmax
- 이 파라미터들은 FLV 함수의 모양을 조정한다. 고급 사용자는 이 값을 바꿔가며 실험할 수 있다; MATLAB 함수 FLV.m을 참조하라. scale 세팅과 비슷하게, 모든 근육들에 대해 FLV 파라미터를 바꾸고 싶다면, default 요소에서 바꾸면 된다.
- Custom model
- 우리의 근육 모델의 파라미터를 바꾸는 대신, general 액추에이터의 gaintype, biastype, dyntype을 "user"로 바꾸고 실행 시간에 콜백을 제공함으로서 사용자는 다른 모델을 구현할 수 있다. 아니면, 이 타입 중에 일부는 "muscle"로 남겨 두어 우리 모델을 쓰고, 다른 요소만 교체할 수 있다. 참고로 tendon 기하학적 계산은 여전히 표준 MuJoCo 파이프라인에 의해 관리되어 사용자의 근육 모델에 actuator_length, actuator_velocity, actuator_lengthrange를 입력으로서 제공한다. 사용자 콜백은 부드러운 tendon의 모델링 등 우리가 무시하기로 한 기타 상세한 사항을 시뮬레이트하는데 쓰일 수 있다.
OpenSim과의 관계성
생체역학계의 연구자들이 사용하는 표준 소프트웨어는 OpenSim이다. 우리는 우리의 근육 모델을 훨씬 더 빠르고 안정적인 시뮬레이션을 하기 위해 조금 단순화하였지만, 그래도 가능한 OpenSim 모델과 비슷하도록 설계했다. MuJoCo 사용자가 OpenSim 모델을 변환하는 것을 돕기 위해, 우리는 비슷한 점과 차이점을 정리했다.
활성화 역학 모델은 기본 시상수값을 포함하여 OpenSim과 동일하다.
FLV 함수는 완전히 같지는 않지만, MuJoCo와 OpenSim은 같은 실험 데이터를 근사하므로, 매우 비슷하다. OpenSim 모델 및 관련된 실험 데이터의 요약에 대한 설명은 Millard et al, "Flexing computational muscle: modeling and simulation of musculotendon dynamics", J Biomech Eng. 2013 Feb;135(2) 를 참조하라.
OpenSim은 부드러운 tendon을 모델링 할 수 있지만 우리는 단단한 tendon을 가정했다.
그 이유는 부드러운 tendon의 모델링은 빠른 평형 가정(fast-equilibrium assumptions)이 필요하며 이는 여러 트윅이 필요하고 따라서 시뮬레이션을 불안정하게 만든다.
실제로 tendon은 꽤나 딱딱하며, 그 효과는 FL 곡선을 적절하게 잡아 늘림으로서 근사할 수 있다 (Zajac 89). 이는 MuJoCo의 근육 동작 범위(range)를 짧게 하는 것과 같다.
회전 각도 (예: 근육과 힘의 작용선 상의 각도)는 MuJoCo에서 모델링되지 않고 0으로 가정한다.
이는 근육의 힘을 적절히 스케일 다운 하고 동작 범위를 조정함으로서 근사할 수 있다.
Tendon 래핑은 MuJoCo에서 더욱 제약된다. 우리는 구와 무한 원기둥을 래핑 물체로 허용하고, tendon 경로 안의 고정된 site에 의해 두 물체가 분리되는 것을 요구한다.
이는 tendon 경로 순차적 계산의 필요성을 피하기 위해서이다.
또한 MuJoCo 2.0에서 우리는 구 또는 원기둥 내부에 위치해야 하는 "side sites"를 허용한다. 이는 tendon 경로가 특정 영역을 지나게 하기 위한 OpenSim의 토러스 래핑 물체를 대체할 수 있다.
전체적으로, tendon 래핑은 OpenSim 모델에서 MuJoCo 모델으로 컨버팅 하기 가장 어려운 부분이며, 약간의 수작업이 필요하다.
밝은 면으로는, 널리 쓰이는 고품질의 OpenSim 모델은 몇 개 없으며, 그것들이 컨버팅 되면 끝이다.
아래에 MuJoCo 2.0에서 가능한 4가지 종류의 tendon 래핑을 묘사해 놓았다.
참고로 래핑된 tendon의 곡선 부분은 직선으로 렌더링되지만, 기하학적 파이프라인은 실제 곡선에 맞게 동작하며, 그들의 길이와 모멘트를 해석적으로 계산한다.
XML 문서 (XML Reference)
actuator/muscle
이 요소는 근육 액추에이터 섹션에서 설명한 대로 근육 액추에이터를 모델링하기 위해 사용된다.
- name: string, optional
- 요소 이름. 이름 요소 섹션 참고.
- class : string, optional
- 기본 클래스. 기본 설정 섹션 참고.
- group : int, "0"
- 액추에이터가 속할 정수 그룹. 이 요소는 커스텀 태그로 사용될 수 있다. 또한 visualizer에서 그룹별 액추에이터 렌더링 활성화/비활성화에도 쓰인다.
- ctrllimited : [false, true], "false"
- true: 이 액추에이터로의 제어 입력은 실행 시간에 ctrlrange 대로 클램핑된다.
- false: 클램핑 비활성화
- 참고로 option flag의 clampctrl 속성으로 제어 입력 클램핑을 전역 비활성화 할 수 있다.
- forcelimited : [false, true], "false"
- true: 이 액추에이터의 힘 출력은 실행 시간에 forcerange 대로 클램핑된다.
- false: 클램핑 비활성화
- ctrlrange : real(2), "0 0"
- 제어 입력의 클램핑 범위. 컴파일러는 첫 번째 값이 두 번째 값보다 작을 것이라 예상한다.
- forcerange : real(2), "0 0"
- 힘 출력의 클램핑 범위. 컴파일러는 첫 번째 값이 두 번째 값보다 작을 것이라 예상한다.
- lengthrange : real(2), "0 0"
- 액추에이터의 전달 길이의 실현 가능한 범위. Length Range 섹션 참고. (역주: 밑의 range와는 다르다. 여긴 정말 물리적으로 가능한 길이의 범위)
- gear : real(6), "1 0 0 0 0 0"
- 이 속성은 모든 전달 타입에 대해 액추에이터의 길이(따라서 모멘트의 팔, 속도 그리고 힘)을 스케일링 한다. 이는 힘 생성 메커니즘에서의 gain과는 다른데, gain은 힘 출력만을 스케일링하고, 길이, 모멘트의 팔, 속도에는 영향을 미치지 않기 때문이다. 스칼라 전달을 가진 액추에이터는, 벡터의 첫 번째 값만 사용된다. 나머지 값들은 3D 힘 및 토크 축을 지정하는데 쓰기 위해서 관절, 부모에서의 관절(jointinparent), site 전달 속성에는 필요하다.
- tendon : string, optional
- 지정되었다면, 주어진 tendon에 액추에이터가 작용한다. 액추에이터 길이는 tendon 길이 * 기어비 이다. Spatial 및 fixed tendond 둘 다에 사용할 수 있다.
- user : real(nuser_actuator), "0 ... 0"
- 사용자 파라미터 섹션 참고.
- timeconst : real(2), "0.01 0.04"
- 활성/비활성 다이나믹스를 위한 시상수이다.
- range : real(2), "0.75 1.05"
- L0 단위로 정의된 근육의 동작 범위. (역주: 위의 lengthrange와는 다르다. 설명상 근육의 동작 가능한 범위라고 나와 있기는 하지만, 거의 L0 및 LT의 계산을 위해 쓰이는 파라미터이다.)
- force : real, "-1"
- 휴식기 최대 동적 힘. 이 값이 음수이면, 최대 힘은 아래의 scale 속성에 의해 자동으로 결정된다.
- scale : real, "200"
- 만약 force 속성이 음수이면, 근육의 최대 동적 힘은 scale / mjModel.actuator_acc 으로 결정된다. mjModel.actuator_acc는 qpos0의 액추에이터 전달에 대해 단위 힘을 적용했을 때 발생하는 관절 공간의 가속도의 norm이다.
- 다시 말해, 스케일링 하면 근육의 최대 힘이 커지고 더 많은 무게를 당기게 한다.
- lmin : real, "0.5"
- L0으로 정규화된 FLV 곡선에서 최저 위치 범위.
- lmax : real, "1.6"
- L0으로 정규화된 FLV 곡선에서 최대 위치 범위.
- vmax : real, "1.5"
- L0/s으로 정규화된 근육의 힘이 0이 될 때의 수축 속도.
- fpmax : real, "1.3"
- lmax일때 생성되는 정적 힘. 휴식기 최대 힘과 관련이 있다.
- fvmax : real, "1.2"
- 포화 수축 속도일때 생성되는 동적 힘. 휴식기 최대 힘과 관련이 있다.
그래서 range, lengthrange 등은 뭐가 다른거냐고?
tendon
- range: tendon의 물리적인 길이 제한. 이 길이 이상으로는 절대로 늘어날 수 없다.
muscle
- lengthrange: muscle의 가동 범위. tendon의 range와는 다르게, 이 근육이 물리 시뮬레이션의 제약을 바탕으로 최대로 늘어날 수 있는 길이를 줘야 한다. (팔에 달린 근육은, 팔의 관절 각도 이상으로 늘어날 수 없다.)
- range: L0 단위로 정의된 근육의 동작 범위. 근육 힘 특성인 L0과 LT의 계산을 위해 쓰인다.